Cryptocurrencies and privacy [part 2]

Privacy-enhancing cryptocurrencies

While the previous blog post concerned itself with privacy-enhancing Bitcoin-compatible protocols, in this one we will analyze a different approach to increase privacy, namely privacy-enhancing cryptocurrencies. The main distinguishing features of them are:

• They improve on older cryptocurrencies by placing privacy at the core of their new design
• They aren’t backward compatible since they’re a whole new cryptocurrency
• They have inherently higher complexity

So far, so good. Those new privacy-enhanced cryptocurrencies sound like a nice deal, what are some real-world examples then? Well, let’s point out the most prominent ones and then analyze them closer. We’ll be scratching on Zerocoin, Zerocash, and Monero.

Zerocoin

The first one, Zerocoin, is more of a protocol-oriented project. Quoting its creators as to what its aim is:

Zerocoin is a project to fix a major weakness in Bitcoin: the lack of privacy guarantees we take for granted in using credit cards and cash. Our goal is to build a cryptocurrency where your neighbors, friends, and enemies can’t see what you bought or for how much.

Zerocoin website

This very cool statement is backed by the mixing capability implemented in the protocol itself. Now, let’s open Zerocoin’s hatch and see how its gears turn. The main idea is that there are two types of coins – a Basecoin (Bitcoin or some other altcoin) and a Zerocoin which serves as an extension of the Basecoin. Basecoins can be swapped for Zerocoins and vice versa. If you go back to the first part of this post, you will see that this serves pretty much the same purpose as coin mixing and it aims to remove the linkability of the initial Basecoins. You can find a rough visualization of what happens when using only the Basecoin vs Basecoin + Zerocoin.

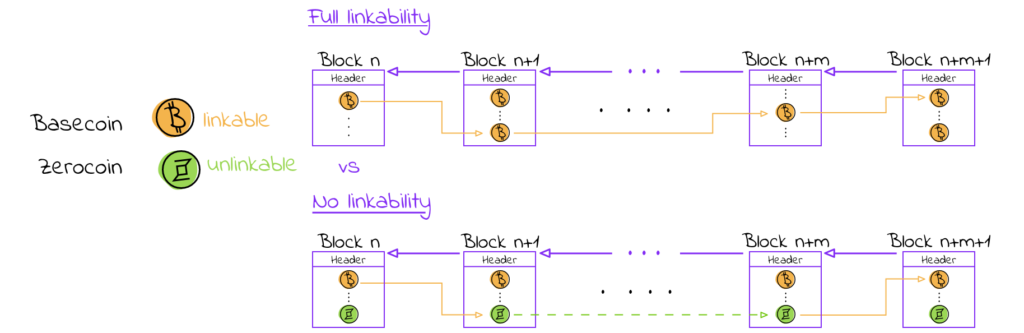
The idea consists of two parts: initially, a user converts a Basecoin into a Zerocoin, and then, in the future, the same user can use the Zerocoin to turn it back into a Basecoin. The protocol guarantees a curious user can’t find out exactly which Zerocoin was used to create a Basecoin, hence the initial “creator” of the Zerocoin can’t be linked. The first part (minting) is achieved through a classical cryptographic commitment. To mint a Zerocoin, a user must generate a serial number S which will be used in the future to spend the Zerocoin (this prevents double-spending), and a random secret r which must remain private (this enforces the unlinkability when spending). The commitment then is calculated as c := g^(S) * h^(r) (g and h being hash functions) which ensures that neither S nor r can be computed by only knowing the commitment c. Once this is done, a user posts the commitment together with the hash of the Basecoin which they wish to convert to Zerocoin, and if the Basecoin is owned by them, then the minting transaction is accepted and posted on the blockchain.

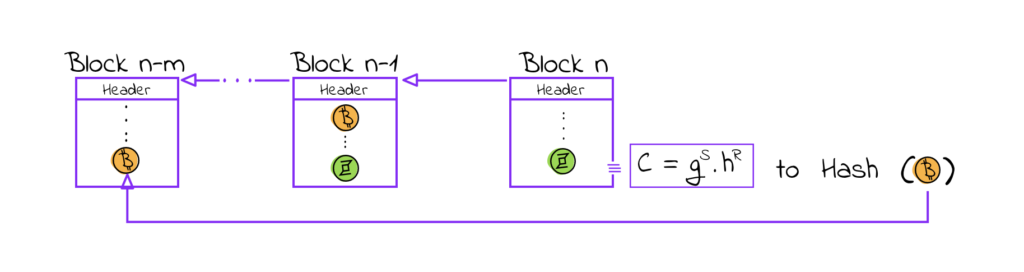
So far, unlinkability hasn’t been achieved. This is done in the second part (spending). To accomplish this, the protocol utilizes several techniques, one of which is an accumulator. A closer look at how accumulators operate is shown below.

Generally, the accumulator in the Zerocoin protocol is used for accumulating every mint transaction on the blockchain as part of the spending phase. So, after this slight technical detour, let’s look at how Alice can spend her Zerocoins while maintaining unlinkability.

1. Firstly, she would have to publish the serial number S she generated at the minting phase – remember that c := g^(S) * h^(r)
2. Then, she should accumulate all previously minted Zerocoins (their commitments) on the blockchain – a
3. After that, Alice will compute the public witness w for her coin
4. Lastly, she must create a ZKP stating that “she knows a random secret r such that a coin c is one of the minted Zerocoins”. She keeps r and c secret, of course.
   
   The ZKP is the interesting part since it uses a logical disjunction of ZKPs for all of the Zerocoins and the whole ZKP is evaluated as true if one ZKP is valid while not revealing exactly which ZKP is valid.

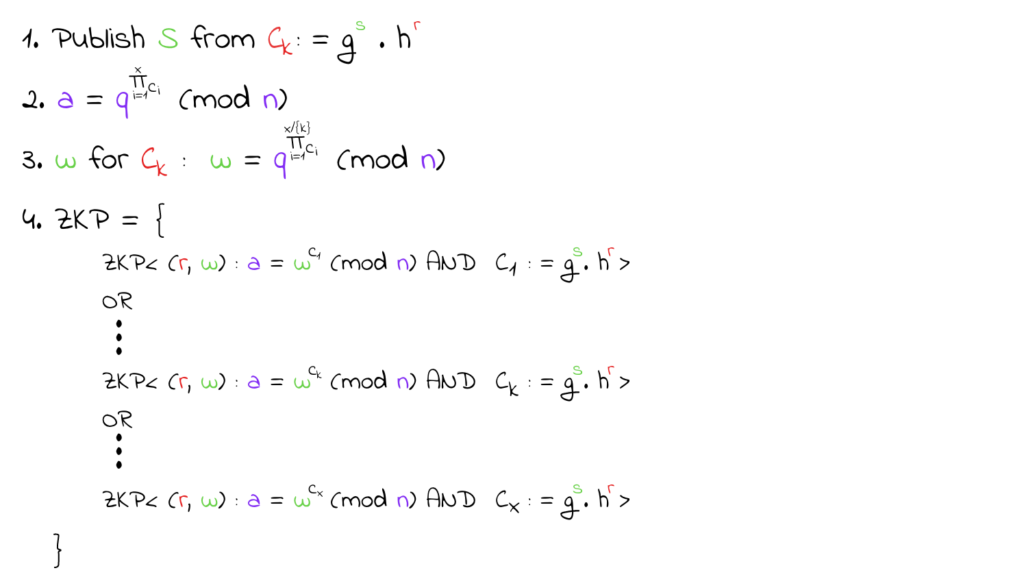
Of course, the protocol itself doesn’t guarantee absolute unlinkability if used poorly. For once, if there are only a few people using Zerocoins, then the overall ZKP from step 4 would result in very fragile unlinkability. Another point of failure is user habits. The effectiveness of the protocol depends on the users making smart decisions, meaning that if a single user mints a Zerocoin from one address and then simply spends a Zerocoin from the same address, nothing is achieved.

Zerocash

If you visit Zerocoin’s official website, you will see the information that the protocol has been succeeded by a fully functional project called Zerocash. So, what are the improvements?

The main change is that Zerocash runs on its own and doesn’t need a Basecoin to function. Additionally, it relies on better cryptographic proof techniques (zk-SNARKs). At its core, Zerocash makes use of the notion that there are 2 address types – private (z-addresses) and transparent (t-addresses) ones which allow 4 different transaction types.

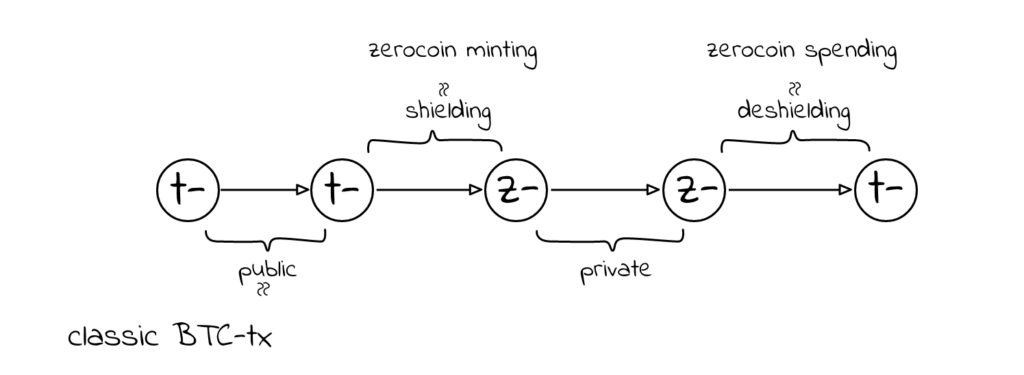
The most interesting of these 4 transaction types If the Z-to-Z transaction which quoting Zerocash’s website is specified as follows:

A Z-to-Z transaction appears on the public blockchain, so it is known to have occurred and that the fees were paid. But the addresses, transaction amount, and the memo field are all encrypted and not publicly visible. This type of encryption is only possible through the use of zero-knowledge proofs.
The owner of an address may choose to disclose z-address and transaction details with trusted third parties — think auditory and compliance needs — through the use of view keys and payment disclosure.

Zerocash website

So far, Zerocash looks better than Zerocoin, but it also has some drawbacks. The main one being the inherent need for a secret random input needed to generate public parameters during the setup phase and the importance of these inputs being securely destroyed. The reason for this is if someone gets ahold of those secrets, then that person could forge coins arbitrarily. This hasn’t happened yet, so we can assume the system has been safe so far.

Monero

But what if we are looking for a cryptocurrency that is even stricter when it comes to privacy. How about something along these lines:

• It’s a set of open-source privacy-focused protocols that were initially built upon Bytecoin/CryptoNode code
• There’s an accepted hard-fork approximately twice a year used as a testing environment for new functions
• The community interest is increasing constantly and it’s very well maintained

Well, this is Monero for you. It has its roots in this famous bitcointalk forum thread. Nowadays, Monero developers have implemented several very important features that make the cryptocurrency arguably the best privacy-oriented one out there: it provides stealth addresses which aren’t the typical public addresses as in other cryptos, the transaction information is confidential meaning the transacted amounts aren’t publicly visible, and it utilizes ring signatures.

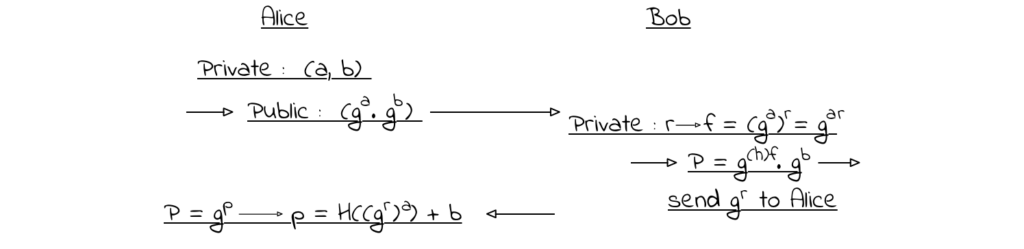
Let’s look at the first feature, stealth addresses. Most cryptocurrencies promote the usage of a new address for every payment, however, this has often proven to be ineffective in maintaining privacy. Firstly, due to the work in modern heuristics that aim to link addresses and secondly, because at some point one user has to communicate an address to another user or service. This is why Monero tackled this problem by creating a new address management system. Stealth addresses function by allowing a user to post a general public “STEALTHADDR” which other users can use as a blueprint to create arbitrarily many different addresses and send coins to them. These coins will be accessible only by the user holding the private key to the blueprint “STEALTHADDR”. This way, a curious user can’t link different fresh addresses to the initial “STEALTHADDR”.

The math behind this isn’t too complex. Let’s say Alice creates a pair of private keys – (a, b) and publishes a pair of public keys – (g^a, g^b). After that, Bob can use those public keys to create as many fresh addresses as he wants and send money to Alice through those. For a new address, Bob generates a private random secret r, computes f = g^(a * r), and then the new address would be P = g^(H(f)) * g^b. When sending coins, Bob also includes g^r. Now, Alice can compute the private key p for the new address P simply by calculating p = H(g^(a * r)) + b and spend the coins.

The next important feature is confidential transactions. Monero has correctly focused on hiding the transacted amount because that piece of information is quite heavily utilized in modern linking heuristic methods. This is achieved via the homomorphic property of commitments (confidential transactions in Monero). Besides the essential hiding and binding properties, the homomorphic one is applied so that if there are, for example, 3 commitments – a single commit for 1 coin, another commit for 4 coins, and another for 6 coins, their combination would result in a single commitment for 11 coins.

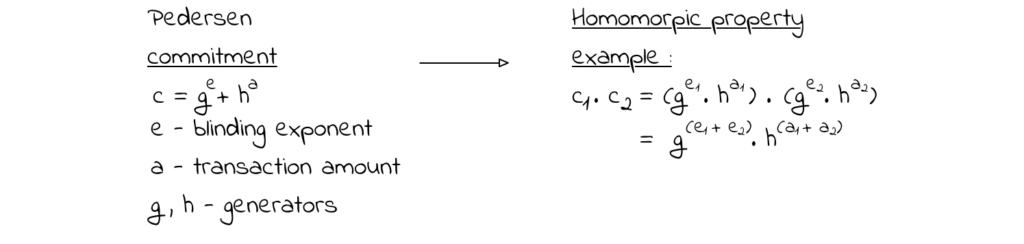
Let’s now apply this to Monero’s confidential transactions in a practical example.

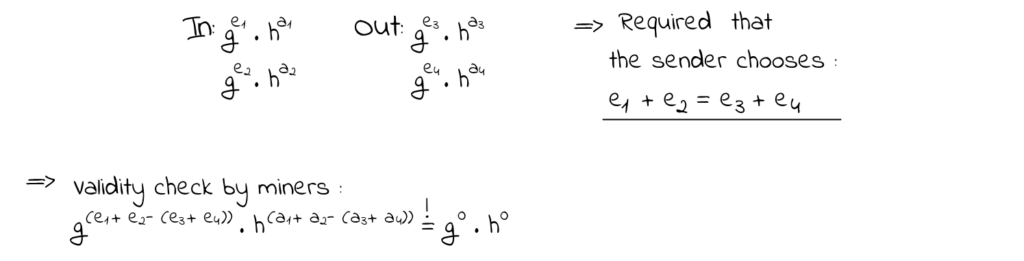
Now, for the last essential part of Monero – ring signatures. To introduce this concept, we can start off with an example of a typical Bitcoin transaction. In it, every input has a deterministic mapping to a single output. This makes the system quite simple and easy to use at the cost of enabling transaction tracking. In contrast to this approach, ring signatures provide a cryptographic mechanism that allows many outputs to be mapped to a single input. Monero basically manages to create a transaction signature via ring signatures that:

• Proves that one of the secret keys was used to make a transaction
• Doesn’t reveal the public key that was used in the transaction
• Prevents the usage of the same public key in future transactions

To best illustrate how this works, imagine that you are given a bucket of lego pieces that can be combined to form a circle. You also have your very own lego piece which is identical to all of the others in the bucket, but only you know that it’s your own piece. Now, you take random pieces from the bucket and, together with your piece, build a circle without anyone looking. You then take the circle, give it to someone and ask them to pick out exactly your piece. Intuitively, the success of the person depends on pure chance – the fewer pieces in the circle, the greater the chance of the person guessing which piece is exactly yours. Not only that, but if you always use the same piece, the person guessing might start noticing it, so that’s why it’s important to also use a different personal piece each time.

This non-technical analogy, while basic, highlights the most essential aspects of ring signatures in Monero. For a short summary of the math behind the mechanism, you could check out the picture below.

Conclusion

The ongoing research focusing on privacy in cryptocurrencies is very active. As presented in the first part of this blog post, there are several viable solutions that focus on making privacy-enhancing technology compatible with current cryptocurrencies. But, many active projects have taken this a step further and succeeded in creating new cryptocurrencies which are all about keeping coin users anonymous.
With the risk of repeating myself, regardless of whether you think anonymity in cryptocurrencies is important or not, privacy is something that shouldn’t be neglected! It’s such a hot topic in today’s tech world for a reason. As long as cryptocurrencies continue to strive towards being a viable and even better alternative to fiat currencies, they have to at least try and be better in every aspect possible. Of course, the physical aspect of cash seems rather impossible to replicate via a blockchain. Privacy, however, is something that could and must be improved and hopefully, developers will continue to improve this aspect of the technology that is the future – cryptocurrencies!